ceres-solver tutorial
ceres-solver tutorial 문서를 공부한 글입니다.
dependency
# CMake
sudo apt-get install cmake
# google-glog + gflags
sudo apt-get install libgoogle-glog-dev libgflags-dev
# BLAS & LAPACK
sudo apt-get install libatlas-base-dev
# Eigen3
sudo apt-get install libeigen3-dev
# SuiteSparse and CXSparse (optional)
sudo apt-get install libsuitesparse-dev
ceres-solver installation
cd catkin_ws/src
git clone https://ceres-solver.googlesource.com/ceres-solver
// git clone 받은 디렉토리 옆에 ceres-bin 생성
mkdir ceres-bin
cd ceres-bin
make -j3
make test
make install
Introduction
\[min \frac{1}{2}\sum_{i}\rho(||f_{i}(x_{i_{1}},\cdots,x_{i_{k}})||^{2})\]Ceres는 $x_{j}$가 어떤 범위 안에 있을 때 non-linear least square 문제를 풀 수 있게 해준다.
\[\rho(||f_{i}(x_{i_{1}},\cdots,x_{i_{k}})||^{2})\]이 ResidualBlock이고, $f_{i}(\cdot)$이 CostFunction,이다. 또한 $x_{i}$ 값들의 집합을 ParameterBlock이라고 한다. $\rho_{i}$는 LossFunction이다.
특별한 케이스로 $\rho_{i}(x)=x$, x값의 범위는 $-infty$ 부터 $infty$까지로 설정한다. 그러면 식을
\[\frac{1}{2}\sum_{i}||f_{i}(x_{i_{1}},\cdots,x_{i_{k}})||^{2}\]로 간단하게 나타낼 수 있다.
Hello world!
cd ceres-bin/bin
//실행
./helloworld
코드는 ceres-solver/examples/helloworld.cc를 보면 된다.
ceres-solver에서 가장 간단한 예제인 Hello wolrd를 통해 $\frac{1}{2}(10-x)^{2}$ 를 최소로 만드는 x값을 구해보자. 우리는 쉽게 x가 10일 때 이 값이 최소가 되는것을 알 수 있지만 이 예제로 ceres의 기본을 배워보자.
struct CostFunctor {
template <typename T>
bool operator()(const T* const x, T* residual) const {
residual[0] = 10.0 - x[0];
return true;
}
};
cost function $f(x)=10-x$로 설정하는 부분이다. template을 써서 어떤 input과 output이 들어오던 T 형태로 받게 된다. residual 값이 double일수도 있고, vector 형태일수도 있기 때문이다.
int main(int argc, char** argv) {
google::InitGoogleLogging(argv[0]);
// The variable to solve for with its initial value. It will be
// mutated in place by the solver.
double x = 0.5;
const double initial_x = x;
initial_x 값을 0.5로 설정한다.
// Build the problem.
Problem problem;
// Set up the only cost function (also known as residual). This uses
// auto-differentiation to obtain the derivative (jacobian).
CostFunction* cost_function =
new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
problem.AddResidualBlock(cost_function, nullptr, &x);
Problem을 선언하고, cost_function에 AutoDiffCostFunction을 통해 미분을 해준다. 만약 residual에 여러 값이 있다면 T=Jet으로 jacobian을 나타내게 된다.
이 cost_function을 ResidualBlock에 넣어 풀게 되면,
// Run the solver!
Solver::Options options;
options.minimizer_progress_to_stdout = true;
Solver::Summary summary;
Solve(options, &problem, &summary);
std::cout << summary.BriefReport() << "\n";
std::cout << "x : " << initial_x << " -> " << x << "\n";
return 0;
}

iteration 2번만에 x값이 10이 나오는 것을 볼 수 있다.
Powell’s Function
cd ceres-bin/bin
./powell

| 위와 같이 cost function이 있다고 할 때, $\frac{1}{2} | F(x) | ^2$ 를 최소화 하는 x를 찾아보자. |
struct F1 {
template <typename T>
bool operator()(const T* const x1, const T* const x2, T* residual) const {
// f1 = x1 + 10 * x2;
residual[0] = x1[0] + 10.0 * x2[0];
return true;
}
};
struct F2 {
template <typename T>
bool operator()(const T* const x3, const T* const x4, T* residual) const {
// f2 = sqrt(5) (x3 - x4)
residual[0] = sqrt(5.0) * (x3[0] - x4[0]);
return true;
}
};
struct F3 {
template <typename T>
bool operator()(const T* const x2, const T* const x3, T* residual) const {
// f3 = (x2 - 2 x3)^2
residual[0] = (x2[0] - 2.0 * x3[0]) * (x2[0] - 2.0 * x3[0]);
return true;
}
};
struct F4 {
template <typename T>
bool operator()(const T* const x1, const T* const x4, T* residual) const {
// f4 = sqrt(10) (x1 - x4)^2
residual[0] = sqrt(10.0) * (x1[0] - x4[0]) * (x1[0] - x4[0]);
return true;
}
};
위처럼 각 residual을 정의해주고,
double x1 = 3.0; double x2 = -1.0; double x3 = 0.0; double x4 = 1.0;
Problem problem;
// Add residual terms to the problem using the using the autodiff
// wrapper to get the derivatives automatically.
problem.AddResidualBlock(
new AutoDiffCostFunction<F1, 1, 1, 1>(new F1), nullptr, &x1, &x2);
problem.AddResidualBlock(
new AutoDiffCostFunction<F2, 1, 1, 1>(new F2), nullptr, &x3, &x4);
problem.AddResidualBlock(
new AutoDiffCostFunction<F3, 1, 1, 1>(new F3), nullptr, &x2, &x3)
problem.AddResidualBlock(
new AutoDiffCostFunction<F4, 1, 1, 1>(new F4), nullptr, &x1, &x4);
초기값 설정해준 뒤, ResidualBlock에 넣어준다.
Initial x1 = 3, x2 = -1, x3 = 0, x4 = 1
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 1.075000e+02 0.00e+00 1.55e+02 0.00e+00 0.00e+00 1.00e+04 0 4.95e-04 2.30e-03
1 5.036190e+00 1.02e+02 2.00e+01 2.16e+00 9.53e-01 3.00e+04 1 4.39e-05 2.40e-03
2 3.148168e-01 4.72e+00 2.50e+00 6.23e-01 9.37e-01 9.00e+04 1 9.06e-06 2.43e-03
3 1.967760e-02 2.95e-01 3.13e-01 3.08e-01 9.37e-01 2.70e+05 1 8.11e-06 2.45e-03
4 1.229900e-03 1.84e-02 3.91e-02 1.54e-01 9.37e-01 8.10e+05 1 6.91e-06 2.48e-03
5 7.687123e-05 1.15e-03 4.89e-03 7.69e-02 9.37e-01 2.43e+06 1 7.87e-06 2.50e-03
6 4.804625e-06 7.21e-05 6.11e-04 3.85e-02 9.37e-01 7.29e+06 1 5.96e-06 2.52e-03
7 3.003028e-07 4.50e-06 7.64e-05 1.92e-02 9.37e-01 2.19e+07 1 5.96e-06 2.55e-03
8 1.877006e-08 2.82e-07 9.54e-06 9.62e-03 9.37e-01 6.56e+07 1 5.96e-06 2.57e-03
9 1.173223e-09 1.76e-08 1.19e-06 4.81e-03 9.37e-01 1.97e+08 1 7.87e-06 2.60e-03
10 7.333425e-11 1.10e-09 1.49e-07 2.40e-03 9.37e-01 5.90e+08 1 6.20e-06 2.63e-03
11 4.584044e-12 6.88e-11 1.86e-08 1.20e-03 9.37e-01 1.77e+09 1 6.91e-06 2.65e-03
12 2.865573e-13 4.30e-12 2.33e-09 6.02e-04 9.37e-01 5.31e+09 1 5.96e-06 2.67e-03
13 1.791438e-14 2.69e-13 2.91e-10 3.01e-04 9.37e-01 1.59e+10 1 7.15e-06 2.69e-03
Ceres Solver v1.12.0 Solve Report
----------------------------------
Original Reduced
Parameter blocks 4 4
Parameters 4 4
Residual blocks 4 4
Residual 4 4
Minimizer TRUST_REGION
Dense linear algebra library EIGEN
Trust region strategy LEVENBERG_MARQUARDT
Given Used
Linear solver DENSE_QR DENSE_QR
Threads 1 1
Linear solver threads 1 1
Cost:
Initial 1.075000e+02
Final 1.791438e-14
Change 1.075000e+02
Minimizer iterations 14
Successful steps 14
Unsuccessful steps 0
Time (in seconds):
Preprocessor 0.002
Residual evaluation 0.000
Jacobian evaluation 0.000
Linear solver 0.000
Minimizer 0.001
Postprocessor 0.000
Total 0.005
Termination: CONVERGENCE (Gradient tolerance reached. Gradient max norm: 3.642190e-11 <= 1.000000e-10)
Final x1 = 0.000292189, x2 = -2.92189e-05, x3 = 4.79511e-05, x4 = 4.79511e-05
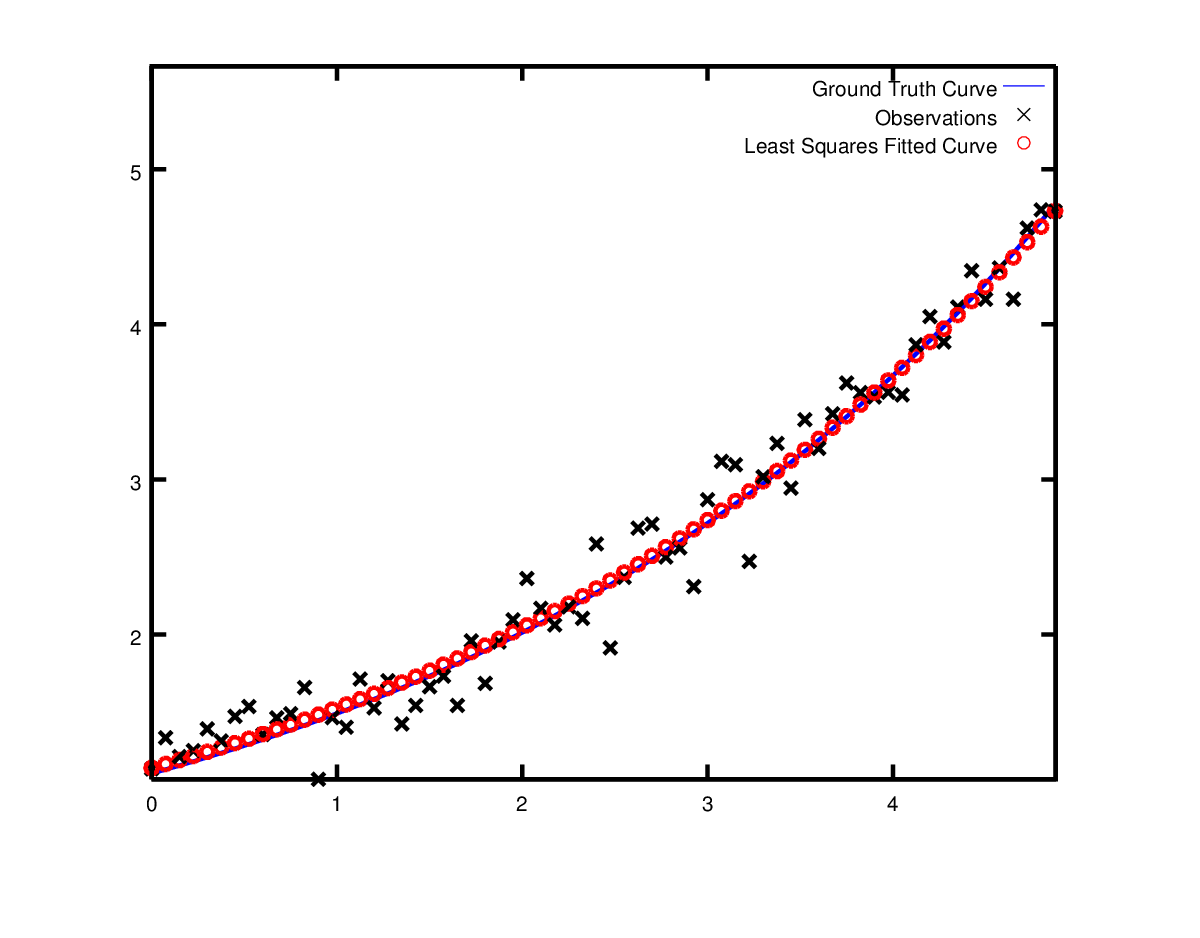
Curve Fitting
위에서는 간단한 optimization을 해보았다면, 이제 실제 데이터를 가지고 curve를 fitting하는 예제를 풀어보자.
\[y=e^{0.3x+0.1}, \sigma=0.2\]$\sigma$는 Gaussian noise
위의 curve를 만들기 위해 $y=e^{mx+c}$라는 모델을 가정하자.
const double data[] = {
0.000000e+00, 1.133898e+00,
7.500000e-02, 1.334902e+00,
1.500000e-01, 1.213546e+00,
2.250000e-01, 1.252016e+00,
3.000000e-01, 1.392265e+00,
3.750000e-01, 1.314458e+00,
4.500000e-01, 1.472541e+00,
5.250000e-01, 1.536218e+00,
6.000000e-01, 1.355679e+00,
6.750000e-01, 1.463566e+00,
넣어줄 데이터의 x,y 값이 쭈르륵 있다. x는 0.075씩 증가하고, y값은
// Data generated using the following octave code.
// randn('seed', 23497);
// m = 0.3;
// c = 0.1;
// x=[0:0.075:5];
// y = exp(m * x + c);
// noise = randn(size(x)) * 0.2;
// y_observed = y + noise;
// data = [x', y_observed'];
다음 식으로 랜덤값을 가지도록 설정한다.
struct ExponentialResidual {
ExponentialResidual(double x, double y)
: x_(x), y_(y) {}
template <typename T>
bool operator()(const T* const m, const T* const c, T* residual) const {
residual[0] = y_ - exp(m[0] * x_ + c[0]);
return true;
}
private:
// Observations for a sample.
const double x_;
const double y_;
};
ExponentialResidual을 위와 같이 정의한다.
실제관측된 y_ 값에서 가정한 모델 $e^{m[0]x_+c[0]}$을 빼서 이 값들의 합이 최소가 되는
m,c를 찾는 것이 목표이다.
double m = 0.0;
double c = 0.0;
Problem problem;
for (int i = 0; i < kNumObservations; ++i) {
CostFunction* cost_function =
new AutoDiffCostFunction<ExponentialResidual, 1, 1, 1>(
new ExponentialResidual(data[2 * i], data[2 * i + 1]));
problem.AddResidualBlock(cost_function, nullptr, &m, &c);
}
위에 있는 넣어줄 데이터를 형태를 맞춰서 x,y값을 data[2*i], data[2*i+1]로 설정해주었다.
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 1.211734e+02 0.00e+00 3.61e+02 0.00e+00 0.00e+00 1.00e+04 0 5.34e-04 2.56e-03
1 1.211734e+02 -2.21e+03 0.00e+00 7.52e-01 -1.87e+01 5.00e+03 1 4.29e-05 3.25e-03
2 1.211734e+02 -2.21e+03 0.00e+00 7.51e-01 -1.86e+01 1.25e+03 1 1.10e-05 3.28e-03
3 1.211734e+02 -2.19e+03 0.00e+00 7.48e-01 -1.85e+01 1.56e+02 1 1.41e-05 3.31e-03
4 1.211734e+02 -2.02e+03 0.00e+00 7.22e-01 -1.70e+01 9.77e+00 1 1.00e-05 3.34e-03
5 1.211734e+02 -7.34e+02 0.00e+00 5.78e-01 -6.32e+00 3.05e-01 1 1.00e-05 3.36e-03
6 3.306595e+01 8.81e+01 4.10e+02 3.18e-01 1.37e+00 9.16e-01 1 2.79e-05 3.41e-03
7 6.426770e+00 2.66e+01 1.81e+02 1.29e-01 1.10e+00 2.75e+00 1 2.10e-05 3.45e-03
8 3.344546e+00 3.08e+00 5.51e+01 3.05e-02 1.03e+00 8.24e+00 1 2.10e-05 3.48e-03
9 1.987485e+00 1.36e+00 2.33e+01 8.87e-02 9.94e-01 2.47e+01 1 2.10e-05 3.52e-03
10 1.211585e+00 7.76e-01 8.22e+00 1.05e-01 9.89e-01 7.42e+01 1 2.10e-05 3.56e-03
11 1.063265e+00 1.48e-01 1.44e+00 6.06e-02 9.97e-01 2.22e+02 1 2.60e-05 3.61e-03
12 1.056795e+00 6.47e-03 1.18e-01 1.47e-02 1.00e+00 6.67e+02 1 2.10e-05 3.64e-03
13 1.056751e+00 4.39e-05 3.79e-03 1.28e-03 1.00e+00 2.00e+03 1 2.10e-05 3.68e-03
Ceres Solver Report: Iterations: 13, Initial cost: 1.211734e+02, Final cost: 1.056751e+00, Termination: CONVERGENCE
Initial m: 0 c: 0
Final m: 0.291861 c: 0.131439
Simple bundle adjuster
BA는 reprojection error를 최소화 시키기 위해 3D point position과 카메라 parameter들을 adjustment하는 것이다.

reprojection error란, 맵 상의 3차원 포인트들을 키프레임 이미지에 투영 시킨 위치와 해당 영상 프레임에서 실제 관측된 위치 차이를 말한다. 이 차이를 최소화 시키는게 BA가 하는 일이다. 카메라 parameter는 extrinsic parameter, intrinsic parameter 두 종류가 있다.
BA example을 돌리기 위해 BAL dataset을 이용한다. 여기서

다음 데이터셋중 하나를 받아서
./simple_bundle_adjuster /경로/txt파일
을 해주면 실행 된다.
gleefe1995@gleefe1995-desktop:~/ceres_ws/src/ceres-bin/bin$ ./simple_bundle_adjuster /home/gleefe1995/ceres_ws/src/ceres-bin/dataset/problem-21-11315-pre.txt
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 4.413239e+06 0.00e+00 8.63e+07 0.00e+00 0.00e+00 1.00e+04 0 2.08e-02 5.28e-02
1 3.542514e+04 4.38e+06 2.40e+06 1.86e+02 9.99e-01 3.00e+04 1 4.46e-02 9.75e-02
2 3.118098e+04 4.24e+03 8.60e+05 1.38e+02 8.90e-01 5.71e+04 1 4.13e-02 1.39e-01
3 3.051581e+04 6.65e+02 1.76e+05 6.77e+01 9.64e-01 1.71e+05 1 4.08e-02 1.80e-01
4 3.042415e+04 9.17e+01 1.48e+05 4.56e+01 9.23e-01 4.36e+05 1 4.28e-02 2.22e-01
5 3.038873e+04 3.54e+01 9.38e+04 5.79e+01 8.99e-01 8.88e+05 1 4.18e-02 2.64e-01
6 3.037939e+04 9.34e+00 2.38e+04 2.97e+01 9.69e-01 2.66e+06 1 4.17e-02 3.06e-01
7 3.037865e+04 7.45e-01 2.66e+03 9.91e+00 9.94e-01 7.99e+06 1 4.26e-02 3.49e-01
Solver Summary (v 2.0.0-eigen-(3.3.4)-lapack-suitesparse-(5.1.2)-cxsparse-(3.1.9)-eigensparse-no_openmp)
Original Reduced
Parameter blocks 11336 11336
Parameters 34134 34134
Residual blocks 36455 36455
Residuals 72910 72910
Minimizer TRUST_REGION
Dense linear algebra library EIGEN
Trust region strategy LEVENBERG_MARQUARDT
Given Used
Linear solver DENSE_SCHUR DENSE_SCHUR
Threads 1 1
Linear solver ordering AUTOMATIC 11315,21
Schur structure 2,3,9 2,3,9
Cost:
Initial 4.413239e+06
Final 3.037865e+04
Change 4.382861e+06
Minimizer iterations 8
Successful steps 8
Unsuccessful steps 0
Time (in seconds):
Preprocessor 0.031990
Residual only evaluation 0.034258 (8)
Jacobian & residual evaluation 0.133728 (8)
Linear solver 0.134065 (8)
Minimizer 0.340961
Postprocessor 0.000913
Total 0.373865
Termination: CONVERGENCE (Function tolerance reached. |cost_change|/cost: 3.371144e-07 <= 1.000000e-06)
BAL problem의 각 residual은 3차원 포인트와 9개의 camera parameter에 depend한다. 3개는 rodrigue’s axis-angle vector, 3개는 translation, 1개는 focal length, 2개는 radial distortion이다.
data format은 다음과 같다.
<num_cameras> <num_points> <num_observations>
<camera_index_1> <point_index_1> <x_1> <y_1>
…
<camera_index_num_observations> <point_index_num_observations> <x_num_observations>
<y_num_observations>
<camera_1> … <camera_num_cameras>
<point_1> … <point_num_points>

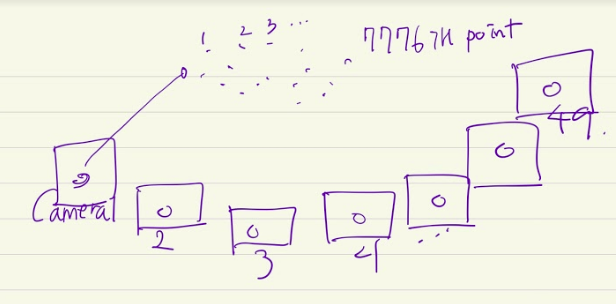
observation 데이터개수, camera pose 데이터개수, 3D point 데이터개수
num_observation + 9*num_cameras + 3*num_points 하면 전체 데이터개수가 나온다.
camera pose는 camera[0~2] -> angle-axis rotation, camera[3~5] -> translation, camera[6] -> focal length, camera[7,8] -> radial distortion이다.
// Read a Bundle Adjustment in the Large dataset.
class BALProblem {
public:
~BALProblem() {
delete[] point_index_;
delete[] camera_index_;
delete[] observations_;
delete[] parameters_;
}
int num_observations() const { return num_observations_; }
const double* observations() const { return observations_; }
double* mutable_cameras() { return parameters_; }
double* mutable_points() { return parameters_ + 9 * num_cameras_; }
double* mutable_camera_for_observation(int i) {
return mutable_cameras() + camera_index_[i] * 9;
}
double* mutable_point_for_observation(int i) {
return mutable_points() + point_index_[i] * 3;
}
bool LoadFile(const char* filename) {
FILE* fptr = fopen(filename, "r");
if (fptr == NULL) {
return false;
};
FscanfOrDie(fptr, "%d", &num_cameras_);
FscanfOrDie(fptr, "%d", &num_points_);
FscanfOrDie(fptr, "%d", &num_observations_);
point_index_ = new int[num_observations_];
camera_index_ = new int[num_observations_];
observations_ = new double[2 * num_observations_];
num_parameters_ = 9 * num_cameras_ + 3 * num_points_;
parameters_ = new double[num_parameters_];
for (int i = 0; i < num_observations_; ++i) {
FscanfOrDie(fptr, "%d", camera_index_ + i);
FscanfOrDie(fptr, "%d", point_index_ + i);
for (int j = 0; j < 2; ++j) {
FscanfOrDie(fptr, "%lf", observations_ + 2 * i + j);
}
}
for (int i = 0; i < num_parameters_; ++i) {
FscanfOrDie(fptr, "%lf", parameters_ + i);
}
return true;
}
private:
template <typename T>
void FscanfOrDie(FILE* fptr, const char* format, T* value) {
int num_scanned = fscanf(fptr, format, value);
if (num_scanned != 1) {
LOG(FATAL) << "Invalid UW data file.";
}
}
int num_cameras_;
int num_points_;
int num_observations_;
int num_parameters_;
int* point_index_;
int* camera_index_;
double* observations_;
double* parameters_;
};
이 txt파일을 BALProblem에서 불러온다.
struct SnavelyReprojectionError {
SnavelyReprojectionError(double observed_x, double observed_y)
: observed_x(observed_x), observed_y(observed_y) {}
template <typename T>
bool operator()(const T* const camera,
const T* const point,
T* residuals) const {
// camera[0,1,2] 회전 행렬
T p[3];
ceres::AngleAxisRotatePoint(camera, point, p);
// camera[3,4,5] 는 tranlation
p[0] += camera[3]; p[1] += camera[4]; p[2] += camera[5];
// Compute the center of distortion. The sign change comes from
// the camera model that Noah Snavely's Bundler assumes, whereby
// the camera coordinate system has a negative z axis.
// camera coordinate가 negative z axis를 갖고 있어서 -를 붙여주는 것 같다.
T xp = - p[0] / p[2];
T yp = - p[1] / p[2];
// Apply second and fourth order radial distortion.
// distortion을 고려
const T& l1 = camera[7];
const T& l2 = camera[8];
T r2 = xp*xp + yp*yp;
T distortion = 1.0 + r2 * (l1 + l2 * r2);
// Compute final projected point position.
// 위에서 계산한 focal, distortion, xp, yp를 가지고 예측된 x,y값을 계산
const T& focal = camera[6];
T predicted_x = focal * distortion * xp;
T predicted_y = focal * distortion * yp;
// The error is the difference between the predicted and observed position.
// 예측값과 실제 관측된 값의 차이 = error
residuals[0] = predicted_x - T(observed_x);
residuals[1] = predicted_y - T(observed_y);
return true;
}
// Factory to hide the construction of the CostFunction object from
// the client code.
static ceres::CostFunction* Create(const double observed_x,
const double observed_y) {
return (new ceres::AutoDiffCostFunction<SnavelyReprojectionError, 2, 9, 3>(
new SnavelyReprojectionError(observed_x, observed_y)));
}
double observed_x;
double observed_y;
};
predicted_x,y : 3D point in world coordinate -> 2D point in camera coordinates (투영된 점)
observed_x,y : 실제 관측된 점
이 두 개의 점의 x,y좌표의 차이를 뺀 것을 residual[0], [1]에 저장한다.
// Create residuals for each observation in the bundle adjustment problem. The
// parameters for cameras and points are added automatically.
ceres::Problem problem;
for (int i = 0; i < bal_problem.num_observations(); ++i) {
// Each Residual block takes a point and a camera as input and outputs a 2
// dimensional residual. Internally, the cost function stores the observed
// image location and compares the reprojection against the observation.
ceres::CostFunction* cost_function = SnavelyReprojectionError::Create(
observations[2 * i + 0], observations[2 * i + 1]);
problem.AddResidualBlock(cost_function,
NULL /* squared loss */,
bal_problem.mutable_camera_for_observation(i),
bal_problem.mutable_point_for_observation(i));
}
위와같이 나타낼 수 있다. curve fitting example이랑 비슷한 부분이 많다.
pose graph 2d
실행방법
여기에서 2d pose graph optimization 데이터셋 하나를 받고
cd ceres-bin/bin
./pose_graph_2d --input /home/gleefe1995/Downloads/input_M3500_g2o.g2o
plot
python3 plot_results.py --optimized_poses ./poses_optimized.txt --initial_poses ./poses_original.txt
matplotlib를 설치하라고 하면
sudo pip3 install matplotlib
파이썬3로 실행했기 때문에 pip3로 설치했다.

참조
http://ceres-solver.org/nnls_tutorial.html#hello-world
