Rodrigues' rotation formula 유도
Rodrigues’ rotation formula
Perspective-n-Points Problem을 공부하다가 Opencv의 solvePnP 함수에서 output으로 나오는 형태가 Rodrigues’s rotation formula를 이용한 표현법으로 나온다고 해서 무엇인지 찾아보았다.
3차원 회전을 다룰 때, Rodrigues’ rotation formula는 한 벡터가 회전할 때 회전 축과 회전 각도가 있으면 다음과 같은 식으로 회전 후의 벡터를 표현하는 방법이다.
\[v_{rot}=vcos\theta+(1-cos\theta)(k\cdot v)k+(k\times v)sin\theta\]그림을 통해 v와 k가 무엇인지 이해해보자.

[그림1]
v 는 $\mathbb{R}^{3}$ 공간의 벡터, k는 회전축 방향의 unit vector이다. v가 k 벡터를 회전축으로 right hand rule을 따라 $\theta$만큼 회전한 벡터가 $v_{rot}$이다.
Derivation
\[v=v_{\parallel}+v_{\perp}\]여기서 $v_{\parallel}=(v \cdot k)k$ 으로 나타낼 수 있고,
\[v_{\perp}=v-v_{\parallel}=v-(k \cdot v)k = -k \times(k \times v)\]으로 나타낼 수 있다.
$v_{\parallel}$은 내적의 정의를 생각하면 쉽게 구할수 있고, $v_{\perp}$은 다음 그림을 통해 구할 수 있다.

[그림2]
이제 $v_{rot}$을 구해보자.
v 벡터가 k를 회전축으로 $\theta$만큼 회전했으니
$v_{\parallel rot}=v_{\parallel}$ 이다.
그리고 v의 크기도 안 바뀌었으니
\[\left | v_{\perp rot} \right |=\left | v_{\perp} \right |\]결국 $v_{\perp rot}$의 방향만 바뀐 것이다.
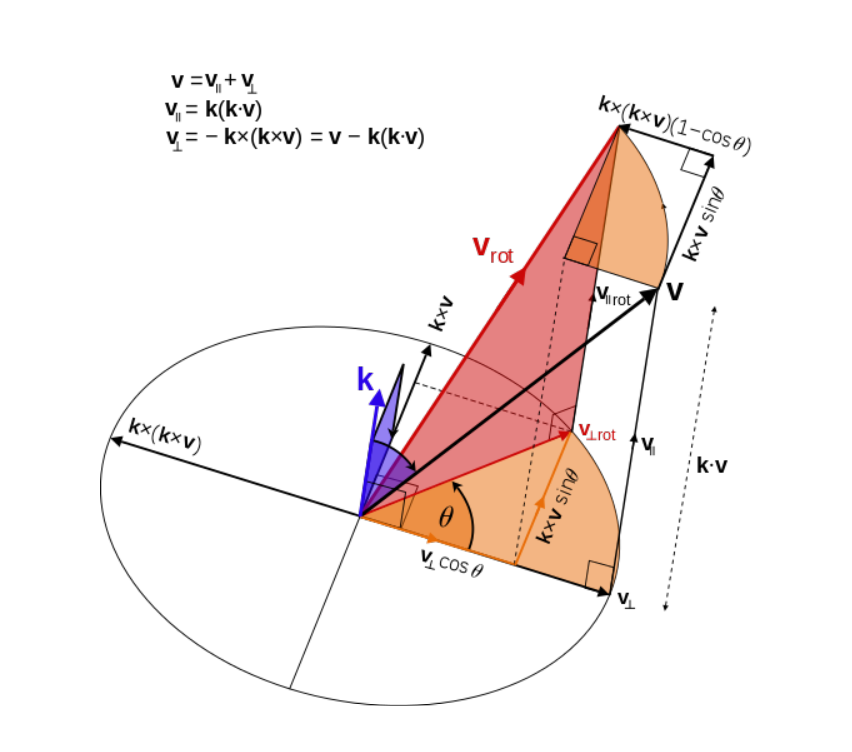
[그림3]
그림3에서 $v_{\perp rot}$을 구해보자.
결론부터 말하면,
$v_{\perp rot}=v_{\perp}cos\theta + (k\times v)sin\theta$
으로 나타낼 수 있는데, 그림3을 이해해보자.
\[\left | v_{\perp} \right |=\left | k\times v \right |=\left | v_{\perp rot} \right |\]이므로
그림3의 원을 그릴 수 있다.
$v_{\perp rot}$을 방향을 잘 생각해서 두 성분으로 나눠보면 이해가 갈 것이다.
$v_{\perp rot}=v_{\perp}cos\theta + (k\times v_{\perp})sin\theta$ 에서
$k\times v_{\parallel}=0$ 이므로 (평행하니까)
$k\times v_{\perp}=k\times(v-v_{\parallel})=k\times v-k\times v_{\parallel}=k\times v$ 로 쓸 수 있다.
따라서, $v_{\perp rot}=v_{\perp}cos\theta + (k\times v)sin\theta$ 로 쓸 수 있다.
그럼 이제 $v_{rot}$을 구해보자.
\[v_{rot}=v_{\parallel rot}+v_{\perp rot},\]$v_{rot}=v_{\parallel}+cos\theta v_{\perp}+ (k\times v)sin\theta$
$=v_{\parallel}+cos\theta(v-v_{\parallel})+(k\times v)sin\theta$
$=vcos\theta+(1-cos\theta)v_{\parallel}+(k\times v)sin\theta$
$=vcos\theta+(1-cos\theta)(k\cdot v)k+(k\times v)sin\theta$
Matrix notation
matrix notation을 알아보자.
먼저, $k\times v$를 column matrices로 나타내보자.
외적을 하면 쉽게 나타낼 수 있다.
\[\begin{bmatrix} (k\times v)_{x}\\ (k\times v)_{y}\\ (k\times v)_{z} \end{bmatrix} =\begin{bmatrix} k_{y}v_{z}-k_{z}v_{y}\\ k_{z}v_{x}-k_{x}v_{z}\\ k_{x}v_{y}-k_{y}v_{x} \end{bmatrix} =\begin{bmatrix} 0 & -k_{x} & k_{y}\\ k_{z} & 0 & -k_{x}\\ -k_{y} & k_{x} & 0 \end{bmatrix}\begin{bmatrix} v_{x}\\ v_{y}\\ v_{z} \end{bmatrix}\]$\mathbf{K}$를 “cross-product matrix”로 정의하면,
\[\mathbf{K}=\begin{bmatrix} 0 & -k_{x} & k_{y}\\ k_{z} & 0 & -k_{x}\\ -k_{y} & k_{x} & 0 \end{bmatrix},\]으로 나타낼 수 있고,
\[\mathbf{K}v=k\times v\]로 나타낼 수 있다.
또한, $\mathbf{K}(\mathbf{K}v)=\mathbf{K}^{2}v=k\times(k\times v)$ 이다.
이제 rodrigues’ rotation formula를 유도할 때 사용했던 식을 이용해서
$v_{rot}$을 matrix 형태로 나타내보자.
우선, 위에서
\[v_{\perp}=v-v_{\parallel}=v-(k \cdot v)k = -k \times(k \times v)\]이러한 식이 있었다.
이 식과 $\mathbf{K}v=k\times v, \mathbf{K}(\mathbf{K}v)=\mathbf{K}^{2}v=k\times(k\times v)$ 를 이용해서 $v_{rot}$을 정리해보자. v와 $v_{\perp}$만 남기면 된다.
$v_{rot}=v_{\parallel rot}+v_{\perp rot}$
$v_{rot}=v_{\parallel}+cos\theta v_{\perp}+ (k\times v)sin\theta$
$v_{rot}=v-v_{\perp}+v_{\perp}cos\theta+(k\times v)sin\theta$
$v_{rot}=v-(1-cos\theta)v_{\perp}+(k\times v)sin\theta$
$v_{rot}=v+(1-cos\theta)\mathbf{K}^{2}v+\mathbf{K}v(sin\theta)$
v로 묶어서 표현해보면,
\[v_{rot}=\mathbf{R}v, \mathbf{R}=\mathbf{I}+(sin\theta)\mathbf{K}+(1-cos\theta)\mathbf{K}^{2}\]으로 나타낼 수 있다.
참고
https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula
