Calibration : Direct Linear Transform

Calibration의 목적은 주어진 2D image point와 3d wrold point pair를 가지고 camera의 extrinsic + intrinsic parameter를 알아내는 것이다.

다음과 같이 $x = PX$로 projection matrix를 나타낼 수 있는데, transformation matrix $P$는 5개의 intrinsic, 6개의 extrinsic parameter를 가지고 있으며 총 11개의 unknown parameter로 구성되어 있다.

homogeneous coordinate으로 쓰게되면 다음과 같이 쓸 수 있고,

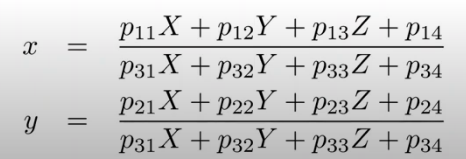
1개의 2d point, 3d point pair 당 위의 두개의 식을 얻을 수 있다.

우리가 모르는 건 P matrix의 unknown paramter 11개 이므로, 최소 6개의 point가 필요하다는 것을 알 수 있다. 이렇게 구하는 것을 Direct Linear Transform이라고 부른다.

$P$ matrix에서 각 행을 A,B,C로 치환한다면

다음과 같이 쓸 수 있게 되고,

위와 같은 식으로 표현할 수 있다.

$p=P^{T}$로 정의하고 $a^T_{x_{i}},a^T_{y_{i}} $를 위와 같이 정의한다면

다음과 같이 표현되게 된다.

즉 우리는 1개의 pair당 x,y에 관한 식 두개가 나오므로 I개의 point에 대하여 위와 같은 형태의 matrix 식을 얻을 수 있게 되고, 이 식은 $Mp$가 최대한 0에 가깝도록 하는 M matrix의 right null space를 구하는 방정식으로 바뀐다.

하지만 모든 point가 같은 plane에 있을 경우(모두 Z=0이라고 가정) rank deficiency가 발생하여 해를 구할 수 없게 된다.

그렇다면 이렇게 구한 $P$ matrix로 부터 어떻게 $K,R,X_{O}$ matrix들을 구할까?

P matrix를 H,h matrix로 나타내게 되면 위와 같다.

우선 camera center$X_{O}=-H^{-1}h$는 다음과 같이 나타낼 수 있다.

Rotation matrix와 K matrix는 $H^_{-1}$ matrix를 QR decomposition을 이용해서 분해하여 얻게된다. Q는 orthogonal matrix, R은 상삼각행렬로, intrinsic matrix가 상삼각행렬이기 때문에 가능하다. 이러한 성질은 inverse matrix에서도 유지되기 때문에 위와 같은 식으로 분해가 가능하다.

H는 homogenous matrix이기 때문에, 이렇게 구한 K matrix 또한 homogenous matrix이다. 따라서 K를 normalize해주기 위해 (3,3) 성분으로 나눠주게 되면 최종적으로 K를 구할 수 있게 된다.