Asynchoronous, Photometric Feature Tracking using Events and Frames
Principle of Operation of event cameras
일반 카메라와 다르게 Dynamic Vision Sensor(DVS)와 같은 이벤트 카메라는 scene의 모든 픽셀의 밝기 변화에 asynchronously and independent 하게 반응한다. DAVIS 같은 이벤트 카메라는 event-based dynamic vision sensor(DVS)와 frame-based active pixel sensor(APS)를 같은 pixel array에 배치하여 각 픽셀의 같은 phtodiode를 공유한다.
각 픽셀은 log intensity를 기억하고 기억된 값에서부터 충분한 변화가 일어났는지를 계속 모니터한다. 정해놓은 threshold를 넘으면, 카메라는 칩에 반영된 x,y 좌표와 시간 t, 그리고 1-bit polarity p (밝기가 증가면 on, 감소하면 off)를 보낸다. 이벤트 카메라는 data-driven sensor이다. 이 카메라의 아웃풋은 밝기 변화나 움직임의 양(amount of motion)에 의해 결정되기 때문이다. 이벤트는 마이크로초 단위로 timestamped 되고 전송되기 때문에 빠른 움직임에도 반응할 수 있다. 픽셀에서 감지된 빛은 scene illumination과 surface reflectance에 의해 생성된 것이다. 만약 조명이 일정하다면 log intensity의 변화는 reflectance의 변화로 나타낸다. 이 reflectance의 변화는 주로 물체의 움직임에 의해서 일어나는데, 이것이 DVS가 밝기변화에 강인한 이유이다.
Abstract
이벤트 카메라와 일반 카메라(우리가 일반적으로 생각하는 카메라)를 서로 상호보완하여 낮은 지연율로 visual feature를 tracking 하는 방법에 대한 논문이다. 이벤트 카메라는 픽셀 레벨에서 “이벤트” 라고 불리는 밝기 변화를 탐지하는 카메라이다. 일반 카메라에 비해 high dynamic range(가장 밝은 곳부터 가장 어두운 데 까지 인간이 보는 것과 가깝게 밝기의 범위가 높다는 뜻), No 모션 블러, 그리고 마이크로초 단위의 지연율(latency)을 가지는 장점이 있다. 하지만, 움직이는 방향에 따라서 같은 scene 에서도 다른 pattern을 보여주기 때문에 event correspondences를 만드는 것이 어렵다. 반대로, 일반 카메라는 밝기 강도를 측정하기 때문에 움직이는 방향에 영향을 받지 않는다. 이 논문에서는 일반 카메라에서와 같이 frame에서 feature를 뽑고, 그 후에 asynchronous(여기서 Asynchronous 하다는 것은 이벤트 카메라가 시간이 아닌 움직일 때 변하는 빛에 의해 작동하기 때문)하게 event를 tracking 한다. 이렇게 하면, 움직이는 방향에 관계 없이 나타낼 수 있고, 또한 지연율도 낮다. 결과적으로, 이 논문에서 제시하는 방법으로 더 넓고 다양한 환경에서 SOTA보다 feature를 더 정확하고 길게 tracking 할 수 있다.
Multimedia Material
A supplemental video for this work is available at https://youtu.be/A7UfeUnG6c4
1 Introduction
이벤트 카메라는 독립적인 픽셀들을 가지고 있고, 밝기 변화가 있을 때만 정보를 보낸다. 따라서 그 output은 밝기 강도 이미지가 아니라 stream of asynchronous events 이다. 이벤트 카메라는 움직임을 캐치하기 때문에 움직임 감지에 뛰어나고, 지연율도 1마이크로초로 매우 낮다. 이벤트 카메라는 일반 카메라 같이 절대적인 밝기 강도를 나타내는 것이 아니고 밝기 변화를 측정한다. 일반 카메라는 모든 픽셀에 대해 직접적으로 밝기를 재지만, 10-20ms의 상대적으로 높은 지연율을 가진다. 이벤트 카메라와 일반 카메라는 이렇듯 상호보완 관계에 있다. 이 둘의 장점을 살리기 위해 Dynamic and Active-pixel Vision Sensor (DAVIS)가 2014년에 도입이 되었다. Asynchronous한 event-based 센서와 일반 frame-based 카메라가 같은 픽셀 array에 위치한 센서이다.
우리는 DAVIS에서 제공한 events와 frames 둘 다 활용하는 feature tracking에서 발생한 문제를 해결하려고 한다. 우리의 목적은 tracking accuracy와 age(feature를 얼마나 오래 tracking 하는지)를 최대화 시키기 위해 두 가지 밝기 타입을 generative event model을 베이스로 한 maximum likelihood approach 방법을 이용하여 재는 것이다.
기존 Feature tracking은 잘 정립되었지만, frame 사이 마다 비어있는 blind time 에는 tracking이 불가하고, 또 움직이지 않을 때도 모든 픽셀의 정보를 처리하기 때문에 너무 expensive 하다. 이벤트 카메라는 tracking과 관련된 정보만 얻고, asynchronously하게 반응하기 때문에 연속된 frame 사이에 blind time을 채울 수 있다.
이 논문에서는 frame에서 corner를 뽑고 그 후에 only events만을 이용하여 feature를 tracking하는 feature tracker를 소개한다. 이것은 asynchronous 하고 high dynamic range, 낮은 지연율의 장점을 가진다. 하지만, 이 asynchronous하다는 점이 data association problem이라고 불리는, 같은 물체로부터 발생한 각각의 이벤트들을 하나로 합쳐야 하는 어려움을 만든다. 이러한 data association 문제를 heuristic하게 풀었던 Previous work와는 다르게 우리는 generative event model을 base로 한 maximum likelihood approach을 소개한다. 이 모델은 위의 문제를 풀기 위하여 frame에서 얻은 photometric information을 사용한다. 정리하면 다음과 같다.
- 밝기 변화의 강도를 이용하고 이벤트와 프레임의 픽셀 사이의 data association 문제를 피하고, 이벤트와 프레임의 밝기 패턴이 어떻게 관련이 있는지 설명하기 위해 generative model을 이용하여 이벤트와 프레임을 결합한 first feature tracker이다.
- SOTA 방법과 비교하여 더 정확하고 길게 tracking하는 방법을 소개한다.
- Event Camera Dataset을 이용하여 tracker를 실험하고 인간이 만든 large contrast(대비) 환경과 자연환경에서 tracking performance도 보여준다.
2 Related work
SOTA는 Canny edges 근처의 grayscale frame에서 Harris corner의 패치를 탐지한다. 그 후 event stream에서 ICP를 이용하여 local edge patterns를 track한다. 따라서, Canny edge patch는 tracking information을 생성하기 위해 등록된 template처럼 행동한다. 문제를 단순화시키기 위해 이벤트가 대부분 strong edges에 의해 생성된다는 가정하에, Canny edgemap template은 이벤트를 만드는 그레이스케일 패턴을 나타낸다. SOTA는 tracking 문제를 geomteric하고 point-set alignment 문제로 변환한다. 이벤트 좌표는 Canny edge의 픽셀 좌표에 의해 주어진 point template과 비교된다. 따라서, 이벤트가 일어나지 않으면, 효율적으로 픽셀은 처리되지 않는다. 하지만 이 방법은 두가지 결점이 있다. 에지의 강도에 대한 정보가 사라진다는 점(tracking을 위한 the point template은 binary edgemap으로 주어지기 때문)과 이벤트와 template 사이의 correspondence를 분리시킨다는 점이다.
우리의 방법도 constrained edge patterns와 반대로 일반적인 특징을 tracking할 수 있다. 하지만, 우리의 방법은 이벤트를 만드는 edge pattern의 강도를 설명할 수 있다는 점, 이벤트와 edgemap template 사이의 correspondence를 만들 필요가 없다는 점에서 SOTA와 다르다. SOTA는 point-set template을 사용했는데, 우리는 spatial gradient of the raw intensity image를 직접적으로 template으로 활용했다.
3 The Challenge of Data Association for Feature Tracking

이벤트 카메라로 Edge patterns와 같은 scene feature를 tracking할 때 main challenge는, 이 센서는 일시적인 밝기 변화에 반응하기 때문에, motion의 방향에 따라 feature가 변한다는 점이다. 그래서 Feature tracking을 할 때는 각기 다른 시간대의 이벤트들간의 correspondence를 잘 정립해야한다.
대신에, Fig.2(a)와 같이 absolute intensity of the pattern같은 추가적인 정보를 얻을 수 있다면(time-invariant한 또는 feature의 map같은 것들), 이벤트 correspondences는 이벤트와 additional map 사이의 correspondences를 정립하여 간접적으로 해결할 수 있다. 하지만, 이 방법은 계속해서 패턴의 optic flow를 측정해야한다. 이 점이 중요한 점인데, 우리 모델은 주어진 frame과 optic flow를 측정하여 time-varying event-feature appearance를 예측한다. 이 generative model은 이전 feature tacking 방법에서는 고려되지 않았던 방법이다.
4 Methodology
이벤트 카메라는 각각의 픽셀이 연속적인 밝기 신호 $L(u,t)$ 의 변화에 반응한다. 여기서 $L \equiv log I$로, logarithmic 변화를 의미한다. 구체적으로, 이벤트 $e_{k}=(x_{k},y_{k},t_{k},p_{k})$ 는 픽셀이 last event와 비교해서 threshold $\pm C$ (with C >0 )만큼 밝기 변화가 생긴다면 픽셀 $u_{k}=(x_{k},y_{k})^{T}$과 시간 $t_{k}$에 일어난다.
\[\Delta L(u_{k}, t_{k})\doteq L(u_{k},t_{k})-L(u_{k},t_{k}-\Delta t_{k})=p_{k}C \cdots(1)\]where $t_{k}$는 같은 픽셀에서 last event로 부터의 시간이고, event polarity $p_{k}$는 -1 또는 1 값으로, 밝기 변화의 sign을 나타낸다. 위의 식은 ideal sensor의 event 생성 equation이다. 여기서
4.1 Brightness-Increment Images from Events and Frames
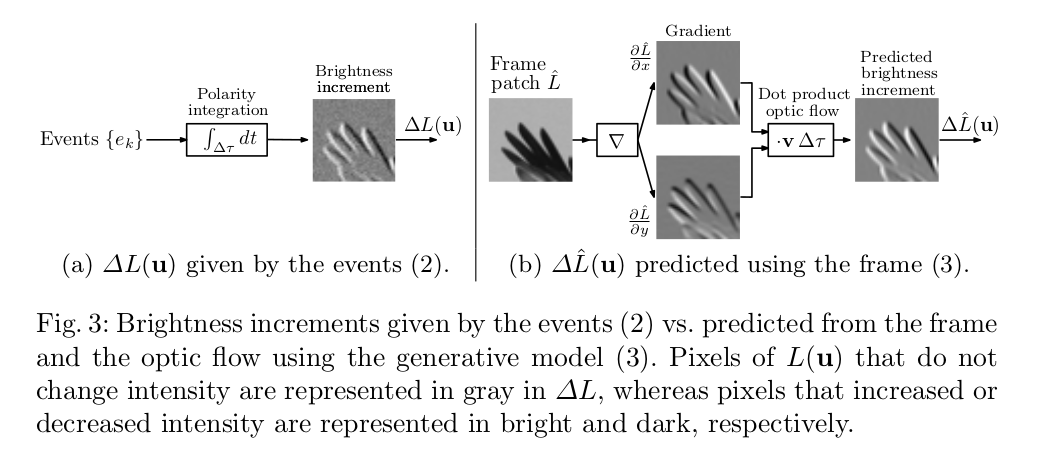
Event polarities의 Pixel-wise accumulation은 Time inverval $\Delta \tau $동안 밝기 변화를 측정하여 image $\Delta L(u)$를 만든다.
\[\Delta L(u)=\Sigma_{t_{k}\Subset \Delta \tau}p_{k}C\delta(u-u_{k}),\cdots(2)\]where $\delta$는 Kronecker delta due to its discrete argument (pixels on a lattice) 이다.
작은 $\Delta \tau$에 대해서, 밝기가 일정하다는 가정 하에
\[\Delta L(u)\approx-\nabla L(u) \cdot v(u)\delta \tau,\cdots (3)\]로 쓸 수 있다. image-point velocity $v \equiv \dot u$이다. 식(2)는 event의 밝기 변화, 식(3)은 frame에서 밝기 변화를 나타낸 것이다. 식(3)의 식을 유도하기 위해서는 먼저 밝기가 일정하다는 가정에서부터 출발한다.
\[L(u(t),t)=const\] \[=>\frac{\mathrm{d} L }{\mathrm{d} t}=\frac{\partial L}{\partial u} \frac{\partial u}{\partial t}+\frac{\partial L}{\partial t} \cdots (3.1)\] \[=>\frac{\mathrm{d} L }{\mathrm{d} t}=\nabla_{u}L \cdot \dot{u}+\frac{\partial L}{\partial t}=0 \cdots(3.2)\]여기서, Taylor expansion을 이용해서 for small $\Delta \tau$에 대해
\[\Delta L(u,t) \doteq L(u,t)-L(u,t-\Delta \tau) \approx \frac{\partial L}{\partial t}(u,t)\Delta \tau \cdots (3.3)\]로 나타낼 수 있고, 식 (3.3)을 (3.2)에 대입하면 식 (3)을 얻을 수 있다. 여기서 u는 point $(x,y)$를 나타내므로 $\nabla L(u)=(\frac{\partial L}{\partial x},\frac{partial L}{\partial y})^{T}$로 나타낸다. 2차원 벡터이기 때문에 dot product로 연산한다. Dot product 특성을 생각해보자. 만약 motion이 edge에 평행하다면, motion은 $\nabla L$과 수직일 것이다($v \perp \nabla L$) .그럼 0이 되어 항이 사라질 것이고 이벤트가 일어나지 않을 것이다. 앞으로는 식(3)을 hat을 써서 $\Delta \hat{L}$로 나타내고 Fig.3(b)에서와 같이 predicted brightness increment라고 부르고, frame은 $\hat{L}$(given at t=0)로 나타낼 것이다.

4.2 Optimization Framework
Maximum likelihood approach를 따라 우리는 optimization score에 따른 이벤트를 설명하기 위한 motion parameter들을 측정하기 위해 관측된 식(2)의 brightness changes $\Delta L$과 식(3)의 predicted 된 $\Delta \hat{L}$의 차이를 사용할 것이다.
더 자세하게, 식(2)와 식(3)을 이용해서 event와 frame의 이미지를 정합(image registration)하는 feature tracking 문제를 풀 것이다. 효과적으로, frame은 이벤트가 등록되는 feature templates처럼 작동한다. 식(2)와 (3)이 구별되는 패턴을 포함한 small patches에서 비교되고, optic flow v는 패치의 모든 픽셀에 대해 일정하다고 가정해보자.
$\hat {L}$은 t=0일 때 intensity frame이고 $\Delta L$은 공간-시간 윈도우의 시간 t가 지난 후의 이벤트에 의해 주어진다. 우리의 목적은 $\Delta L(u)$와 $\Delta \hat{L}(u;p,v)=-\nabla \hat{L}(\mathbf{W}(u;p)) \cdot v\Delta \tau$, where W 은 정합을 위해 사용되는 warping map, 사이의 similarity를 극대화 시킬 수 있는 registration parameters p와 속도 v를 구하는 것이다. 우리는 approximation error가 발생하지 않도록 하고 past noisy features positions에서의 오류 전파를 피하기 위해서 과거 정합 parameter의 차이에 의해 근사하는 대신 optic flow v를 명시적으로 모델링한다. 아래의 Block diagram은 두 brightness increments가 어떻게 계산되는지 보여준다.

$\Delta L - \Delta \hat{L}$이 zero-mean additive Gaussian distribution을 따른다고 가정하면, 우리는 event의 집합
\[\varepsilon \doteq \left \{ e_{k} \right \}^{N_{e}}_{k=1}\]의 likelihood function은
\[p(\varepsilon \mid p,v,\hat{L})=\frac{1}{\sqrt{2 \pi \sigma^{2}}}exp(-\frac{1}{2\sigma^{2}}\int_{P}(\Delta L(u)-\Delta\hat{L}(u;p,v))^{2}du) \cdots(4)\]이다.
Maximizing this likelihood with respect to the motion parameters p and v ($\hat{L}$은 알려져 있기 때문에) yields the minimization of the $L^{2}$ norm of the photometric residual,
\[\min_{p,v}\left \| \Delta L(u)-\Delta \hat{L}(u;p,v) \right \|^{2}_{L^{2}(P)}\cdots(5)\]where $\left | f(u) \right |^{2}{L^{2}(P)} \doteq \int{P}f^{2}(u)du$. 하지만, objective function (5)는 보통 사전에 알려지지 않는 contrast sensitivity C에 의존한다. 그래서 다음과 같은 unit-norm patches를 제안한다.

which cancels the terms in C and $\Delta \tau$, 그리고 feature velocity $v$의 방향에만 의존한다. 우리는 W를 단순화시키기 위해서 rigid-body motion이라고 생각한다.
\[W(u;p)=R(p)u+t(p)\cdots (7)\]where $(R,t)\in SE(2)$. The objective function (6)는 Ceres software에서 제공하는 non-linear least squares framework로 최적화된다.

4.3 Discussion of the Approach
제안된 식 (6)의 가장 흥미로운 성질은 이것이 generative model for the events를 기반으로 하고 있다는 것이다. Fig(5)에서 볼 수 있듯이, the frame $\hat{L}$은 registration template $\Delta \hat{L}$을 만든다. $\Delta \hat{L}$은 motion-dependent한 event data $\Delta L$에 최대한 맞추기 위해 v에 따라 달라지고, 그래서 우리의 방법은 event feature의 warping parameters 뿐만 아니라 optic flow도 추정한다. 이 optic flow dependency는 전의 논문들에서는 명쾌하게 모델화되지 않았다. 더 나아가, 템플릿에서는, 우리는 full gradient information of the frame $\nabla \hat{L}$을 사용하는데, 이는 Canny version보다 더 낮은 정확도를 갖지만 더 중요한 패턴을 tracking 한다.
또 다른 특성 하나는 우리의 방법은 ICP-method와 다르게 event-to-feature correspondences를 설정해야하는 문제에서 벗어났다는 것이다. 우리는 이벤트에서 좀 더 편리한 이미지 표현을 만들어 image registration 방법의 전형적인 픽셀-픽셀 data association을 차용한다. 그리고 이것은 local minima에 빠질 확률이 낮아 더 robust하다.
추가로, minimum cost values를 모니터링하는 것은 feature tracking loss를 발견하고 새 feature를 tracking 하는데 더 견고한 기준을 제공한다.
4.4 Algorithm

Algorithm 1은 두 가지 phase로 이루어져 있다. (i) feature patch의 초기화 (ii) 식 (7)에 따라 patch의 패턴을 tracking 하는 부분이다. 많은 patch들은 patch $\Delta L(u)$를 계산하기 위해 각각 tracking 되고, 우리는 fixed time $\Delta \tau$ 보단 number of event $N_{e}$ 로 적분한다. 따라서, tracking은 asynchronous한데, 이것은 $N_{e}$ event가 보통 일반 카메라보다 더 높은 frame rate로 얻어지기 때문이다.
4.5 Connection with the Lucas-Kanade Method

식(6)은 KLT tracker의 확장판이라고도 해석될 수 있다.
Lucas-Kanade Lucas-Kanade 방법의 목적은 image I와 warp W(u;p)에 의해 이동한 T 사이의 photometric error를 줄이는 것이다.

이것은 Non-linear least-squares(NLLS) 문제이다. 이 문제는 Taylor’s expansion으로 구성된 Gauss-Newton’s method에 의해 풀렸다.

Our proposal 식 (6)은 KLT method 처럼 photometric error를 최소화 시킨다. 하지만, 식(6)의 목적은 두 개의 밝기 변화 이미지를 register하는 것이다. 하나는 축적되는 event에 의해 render 되는 이미지, 다른 하나는 frame의 밝기 gradient에 의해 계산된 것이다. 이것은 motion에 의해 결정되는 feature의 모습과 geometric transformation W 두개 모두를 최적화를 요구한다. Motion(optical flow)는 모르기 때문에, 우리는 축적된 event에 의해 얻어진 이미지를 가장 잘 표현할 수 있는 geometric distortion과 예측된 이미지 모습을 찾기 위해 동시에 warp parameters p와 v를 변화시킨다.

with respect to the augmented parameter vector $\tilde{p} \doteq (p^{T},v^{T})^{T} \in \mathbb{R}^{M+2}$ , 여기서 Gauss-Newton 방법으로 phtometric error를 최소화시킬 수 있다. 이것은 linear system $\tilde{A} \Delta q=\tilde{b}$ 식을 만들 수 있고, M+2는 v가 두 개의 미지수를 가지고 있기 때문이다. $\tilde{p}$의 두 성분 p와 v는 따라서 jointly estimated 된다. 그래서 우리는 이것은 event-based KLT, EKLT라고 이름을 지었다.
Reference
(Gallego, G., Delbrück, T., Orchard, G., Bartolozzi, C., Taba, B., Censi, A., … Scaramuzza, D. (2019). Event-based vision: A survey. ArXiv, 1–30. https://doi.org/10.1109/tpami.2020.3008413)
Gehrig, D., Rebecq, H., Gallego, G., & Scaramuzza, D. (2018). Asynchronous, photometric feature tracking using events and frames. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 11216 LNCS, 766–781. https://doi.org/10.1007/978-3-030-01258-8_46
Gehrig, D., Rebecq, H., Gallego, G., & Scaramuzza, D. (2020). EKLT: Asynchronous Photometric Feature Tracking Using Events and Frames. International Journal of Computer Vision, 128(3), 601–618. https://doi.org/10.1007/s11263-019-01209-w
